Использование кругов Эйлера в различных видах деятельности с дошкольниками
Манапова Майгуль Сагындыковна
Воспитатель высшей категории
КГКП ясли сада №2 «Балдырган»
г.Экибастуза Павлодарской области
Актуальность методических рекомендаций определяется их направленностью на реализацию развивающей функции образования, что является ключевой задачей современной образовательной ситуации в целом и в дошкольном образовании в частности.
Методические рекомендации призваны расширить представления о содержании, сферах использования и образовательных эффектах метода наглядного моделирования для развития логического мышления детей дошкольного возраста.
Содержание методических рекомендаций включает в себя:
– Описание метода наглядного моделирования с помощью кругов Эйлера.
– Этапы овладения действием наглядного моделирования с помощью кругов Эйлера.
– Методические советы по организации образовательной деятельности детей.
Практическая значимость предлагаемых методических рекомендаций для педагогов связана с включением в их содержание конкретных примеров работы с использованием метода наглядного моделирования с помощью кругов Эйлера.
В современных условиях от ребенка требуется не только владение знаниями, но и умение добывать эти знания самому и оперировать ими. Одна из главных задач современной педагогики – это поиск возможностей использования скрытых резервов умственной деятельности детей, поиск путей эффективного обучения. И в сфере образования процесс обучения неизбежно должен быть более наглядным и динамичным. Одним из таких путей, интенсивно развивающим детское познание, может стать моделирование.
Приемы моделирования особенно эффективны для дошкольников, так как у них развито наглядно-действенное мышление, память носит непроизвольный характер, а мыслительные задачи решаются с преобладающей ролью внешних средств, наглядный материал усваивается лучше вербального. Метод наглядного моделирования помогает ребенку зрительно представить абстрактные понятия научиться работать с ними.
В работе наглядное моделирование, позволяет предотвратить быструю утомляемость, создать интерес к занятиям, научить детей видеть главное, систематизировать полученные знания.
Дети очень легко и быстро понимают разного рода схематические изображения и с успехом пользуются ими.
Одну практичную и удобную модель для решения логических задач предлагает выдающийся ученый Леонард Эйлер.
Круги Эйлера – это графическая модель, с помощью которой можно наглядно отобразить отношения между понятиями или множествами объектов. А народная мудрость гласит: «Лучше один раз увидеть, чем сто раз услышать». Учитывая простоту и наглядность модели кругов Эйлера, она с успехом используется в детских садах.
Используя круги Эйлера, ребенок овладевает следующими элементами логических действий:
– анализ объектов с целью выделения признаков;
– синтез – составление целого из частей;
– выбор критериев для сравнения, классификации объектов;
– выведение следствий;
– установление причинно-следственных связей;
– построение логической цепи рассуждений.
Метод наглядного моделирования с помощью кругов Эйлера чаще всего используется для познавательного развития дошкольников.
Начиная с 4-5 лет детям доступно решение простейших задач с кругами Эйлера, сначала с разъяснениями взрослых, а потом и самостоятельно. С детьми этого возраста уместны простые игры и упражнения, цель которых – закрепление представлений о свойствах предметов и геометрических фигур, тренировка в сравнении предметы по цвету, форме, размеру.
Овладение действием наглядного моделирования с помощью кругов Эйлера по формированию элементарных математических представлений лучше начать со сравнения предметов, у которых присутствует один общий признак (например, форма, цвет, размер, толщина), позже можно брать два и более признака, в зависимости от индивидуальных особенностей ребенка.
Для начала вы объясняете детям пространственные понятия «внутри круга» и «вне круга». Важно научить ребенка использовать частицу НЕ для обозначения признака предметов вне круга.
Воспитатель кладет на пол обруч, обводит указкой то место, которое находится внутри обруча и рассказывает, что вся остальная часть пола находится вне обруча. Цель работы с одним кругом – учить классифицировать предметы по одному признаку, понимать и применять логическую операцию отрицания НЕ, не называя её.
У каждого ребенка в руке один предмет. Дети по очереди располагают предметы в соответствии с заданием воспитателя. Расположите внутри обруча – все игрушки, а вне обруча – все остальные предметы. Затем проводится беседа по следующим вопросам:
– Какие предметы лежат внутри обруча? (игрушки)
– Какие предметы оказались вне обруча?
Неправильно, если дети начинают перечислять все предметы вне обруча.
– Выразите свойство всех фигур, лежащих вне круга, одним словом. (Не игрушки)
Важно то, что внутри обруча лежат игрушки, и никаких других предметов там нет.
Затем мы приступаем к распределению предметов на два круга.
Мы объясняем понятия «внутри круга» и «вне круга», используя уже два признака.
Дети выполняют эти простые задания:
– Положите внутрь красного круга треугольные фигуры.
– Положите внутрь синего круга красные фигуры.
После того как все фигуры размещены, воспитатель задает два новых вопроса:
– Какие геометрические фигуры лежат внутри красного круга? (Внутри круга лежат треугольные фигуры).
– Какие геометрические фигуры лежат внутри синего круга? (Внутри круга лежат красные фигуры).
Этот ответ содержится в самом условии только что решенной задачи и формулируется обычно без особого труда. Правильного ответа на второй вопрос приходится ждать дольше.
– Какие геометрические фигуры лежат вне круга? Выразите свойство всех фигур, лежащих вне круга, одним словом. (Вне круга лежат НЕ треугольные, НЕ красные фигуры).
Наша цель в данном случае – охарактеризовать свойство фигур, лежащих вне круга, через свойство фигур внутри круга.
С дошкольниками можно использовать несколько моделей кругов:
а) Непересекающиеся круги;
б) Пересекающиеся круги;
в) Один круг вложен в другой.
Цель работы над задачами с двумя кругами – развить умение классифицировать предметы по двум свойствам, понимать и применять логическую операцию конъюнкции.
Теперь дети будут работать с двумя кругами или обручами разных цветов (синий, красный) с пересекающимися областями.
Перед решением задач необходимо выполнить ряд упражнений. Лучше всего такие упражнения проводить на групповых занятиях с использованием обручей.
– Обведите границу области внутри синего, но вне красного круга.
– Обведите границу области внутри красного, но вне синего круга.
– Обведите границу области внутри синего и внутри красного кругов.
– Обведите границу области вне синего и вне красного кругов.
После успешного выполнения подготовительных упражнений можно приступить к решению задач.
После задачи с расположением фигур дети отвечают на четыре вопроса:
Какие фигуры лежат:
– внутри обоих кругов;
– внутри синего, но вне красного круга;
– внутри красного, но вне синего круга;
– вне обоих кругов?
Фигуры надо называть, опираясь на два свойства – цвет и форму.
Наряду с логическими задачами можно ставить и задачи подсчета фигур.
Сколько фигур лежит:
– внутри обоих кругов;
– внутри синего, но вне красного круга;
– внутри красного, но вне синего круга;
– вне обоих кругов?
Можно усложнить вопрос, добавив к подсчету фигур их признак:
Сколько зеленых фигур лежит вне обоих кругов?
Дети работают с двумя кругами или обручами разных цветов (синий, красный), и размера (большой, маленький) вместо пересечения двух кругов, когда можно положить маленький круг в большой. В один из кругов дети кладут картинки с неживыми предметами, в пересечении кругов находятся карточки с транспортом. Обращаю внимание детей на то, что транспорт не может быть живым, он всегда будет находиться в круге с неживыми предметами. Поэтому вместо пересечения двух кругов, можно положить маленький круг в большой.
Выполняя упражнение дети задумываются: если все объекты первого множества входят и во второе множество, то модель будет представлять собой вложенные круги.
Формирование умения понимать отношения между числами в пределах 5 с помощью кругов Эйлера лучше начинать рассматривать со средней группы, постепенно усложняя их в старшей и подготовительной группе.
Для наиболее способных детей существуют сложные задачи.
Метод наглядного моделирования с помощью кругов Эйлера можно использовать и в речевом развитии дошкольников.
Образная, богатая синонимами, дополнениями и описаниями речь у детей дошкольного возраста – явление очень редкое. В речи детей существуют множество проблем.
Поэтому педагогическое воздействие при развитии речи дошкольников – очень сложное дело. Необходимо научить детей связно, последовательно, грамматически правильно излагать свои мысли, рассказывать о различных событиях из окружающей жизни.
Дошкольники с различными речевыми нарушениями испытывают значительные трудности в усвоении как программы дошкольного образования, так и в дальнейшем программы обучения общеобразовательной школы. Работая с детьми, педагогу приходится искать вспомогательные средства, облегчающие, систематизирующие и направляющие процесс усвоения детьми нового материала.
Такими средствами являются графические модели с использованием кругов Эйлера.
Элементами описательного рассказа являются качественные характеристики объекта:
- принадлежность к родовидовому понятию;
- величина;
- цвет;
- форма;
- составляющие детали;
- качество поверхности;
- материал, из которого изготовлен объект (для неживых предметов);
- как он используется (какую пользу приносит)
- за что нравится (не нравится)
Сначала ребенок составляет модель описания предметов по плану. При этом символы описания (пиктограммы) выкладываются в обручи.
Затем в пересечении кругов выделяются одинаковые признаки предметов. Теперь можно составлять описательный рассказ по данной схеме, определяя сначала сходство, а затем различия предметов.
Например, сравнительное описание собаки и кошки.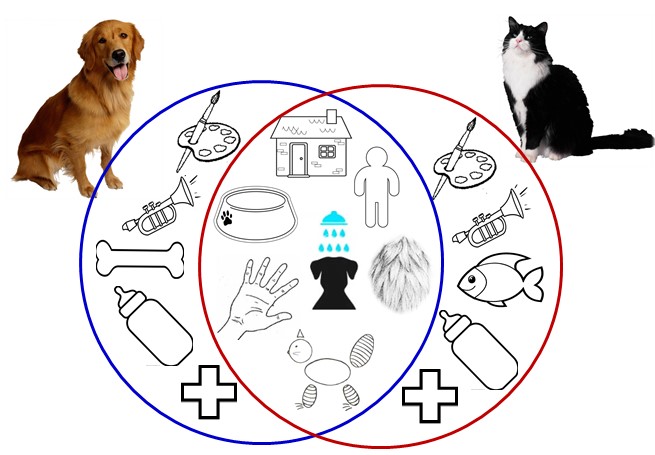
Для начала мы выделяем одинаковые признаки: «Кошка и собака – это домашние животные. О них заботится человек. Он их кормит, ухаживает за ними. Тело кошки и собаки покрыто шерстью. У этих животных есть голова, туловище, уши, хвост, лапы». Затем выделяем различия: «Кошка бело-черного цвета, а собака – рыжего. Кошка мяукает, а собака – лает. Кошка любит пить молоко, есть рыбу, а собака грызть кости. Кошка и собака приносят пользу человеку. Собака охраняет дом, а кошка ловит мышей».
Метод наглядного моделирования с помощью кругов Эйлера можно использовать при ознакомлении дошкольников с окружающим миром.
Детям предлагается набор карточек для решения задач. Например:
- Разложить карточки так, чтобы в одном круге лежало все съедобное, а в другом – фрукты (один круг вложен в другой). Дети определяют предметы, подходящий под описания кругов. Важно обратить внимание ребенка на те, качества, которые присущи объекту всегда.
- Разложить карточки так, чтобы в одном круге были фрукты, а другом – овощи (непересекающиеся круги). Дети определяют предметы, подходящий под описания кругов.
- Разложить карточки так, чтобы в одном круге были все фрукты, а в другом – все красные предметы (пересекающиеся круги, в пересечении – карточка с яблоком). Сначала дети определяют предмет, подходящий под описания кругов. Каждой из пересекающихся окружностей присваивается какое-либо качество. Затем необходимо найти объект, подходящий под описание тех кругов, которые имеют общее пересечение.
Во время следующих занятий детям можно предлагать и более сложные задачи, когда в пересечении двух кругов может оказаться не одна, а несколько карточек.
Итак, в данной методической разработке были рассмотрены основные действия, которые можно производить с множествами, изучены возможности их применения для решения задач, получены методические советы по организации образовательной деятельности детей.
Используя в работе с детьми данную технологию, мы способствуем развитию у них умений анализировать объекты с целью выделения признаков, осуществлять анализ и синтез, то есть составлять целое из частей, в том числе самостоятельно достраивая множества недостающими компонентами, умений сравнивать и классифицировать, обобщать, делать выводы и умозаключения, строить логические цепочки, рассуждать.
Это означает, что мы вооружаем детей необходимыми инструментами для дальнейшего успешного обучения в школе. Учиться станет легче, а значит, и процесс учебы, и сама школьная жизнь будут приносить радость и удовлетворение.
